Go to the Next or Previous section, the Detailed Contents, or the FS(E)L Home Page.
5.2.2.1 Computing semantic equivalence
Two nodes that are identified by strong node-labelled bisimulation are
always semantically equivalent in each of our models.
The models do, however, represent much weaker equivalences and there may
well be advantages in factoring the transition system by the appropriate
one.
The only disadvantage is that the computation of these weaker
equivalences is more expensive: it requires an expensive form of
normalisation, so
-
there may be systems where it is impractical, or too expensive, to
compute semantic equivalence, and
-
when computing semantic equivalence, it will probably be to our
advantage to reduce the number of states using other techniques first
(see 5.2.2.3 Combining techniques).
To compute the semantic equivalence relation we require the entire
normal form of the input GLTS T.
This is the normal form that includes a node equivalent to each node of
the original system, with a function from the original system which
exhibits this equivalence (the map need neither be injective [because
it will identify nodes with the same semantic value] nor surjective
[because the normal form sometimes contains nodes that are not
equivalent to any single node of the original transition system]).
Calculating the entire normal form is more time-consuming that ordinary
normalisation.
The latter begins its normalisation search with a single set (the
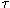 -closure
of T's root,
-closure
of T's root,
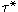 (R)),
but for the entire normal form it has to be seeded with
{
(R)),
but for the entire normal form it has to be seeded with
{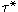 (N) |
N
(N) |
N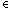 T}),
-- usually as many sets as there are nodes in T.(14)
As with ordinary normalisation, there are two phases: the first
(pre-normalisation) computing the subsets of T that are reachable
under any trace (of visible actions) from any of the seed nodes, with a
unique-branching transition structure over it.
Because of this unique branching structure, the second phase, which is
simply a strong node-labelled bisimulation over it, guarantees to
compute a normal form where all the nodes have distinct semantic
values.
We distinguish between the three semantic models as follows:
T}),
-- usually as many sets as there are nodes in T.(14)
As with ordinary normalisation, there are two phases: the first
(pre-normalisation) computing the subsets of T that are reachable
under any trace (of visible actions) from any of the seed nodes, with a
unique-branching transition structure over it.
Because of this unique branching structure, the second phase, which is
simply a strong node-labelled bisimulation over it, guarantees to
compute a normal form where all the nodes have distinct semantic
values.
We distinguish between the three semantic models as follows:
-
For the traces model, neither minimal acceptance nor divergence
labelling is used for the bisimulation.
-
For the stable failures model, only minimal acceptance labelling is
used.
-
For the failures-divergences model, both sorts of labelling are used and
in the pre-normalisation phase there is no need to search beyond a
divergent node.
The map from T to the normal form is then just the composition of
that which takes N to the pre-normal form node
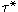 (N),
and the final bisimulation.
(N),
and the final bisimulation.
The equivalence relation is then simply that induced by the map: two
nodes are equivalent if and only if they are mapped to the same node in
the normal form.
Go to the Next or Previous section, the Detailed Contents, or the FS(E)L Home Page.
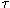 -closure
of T's root,
-closure
of T's root,
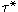 (R)),
but for the entire normal form it has to be seeded with
{
(R)),
but for the entire normal form it has to be seeded with
{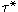 (N) |
N
(N) |
N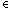 T}),
-- usually as many sets as there are nodes in T.(14)
As with ordinary normalisation, there are two phases: the first
(pre-normalisation) computing the subsets of T that are reachable
under any trace (of visible actions) from any of the seed nodes, with a
unique-branching transition structure over it.
Because of this unique branching structure, the second phase, which is
simply a strong node-labelled bisimulation over it, guarantees to
compute a normal form where all the nodes have distinct semantic
values.
We distinguish between the three semantic models as follows:
T}),
-- usually as many sets as there are nodes in T.(14)
As with ordinary normalisation, there are two phases: the first
(pre-normalisation) computing the subsets of T that are reachable
under any trace (of visible actions) from any of the seed nodes, with a
unique-branching transition structure over it.
Because of this unique branching structure, the second phase, which is
simply a strong node-labelled bisimulation over it, guarantees to
compute a normal form where all the nodes have distinct semantic
values.
We distinguish between the three semantic models as follows: