Benchmarking Collision Detection Algorithms




It is extremely difficult to evaluate and compare collision detection algorithms, because in general they are very sensitive to specific scenarios, i.e., the relative size of the two objects, the relative position to each other, the distance, etc.

Benchmark procedure

I propose a simple benchmark procedure which (hopefully) eliminates these effects. It has been kept very simple so that other researchers can easily reproduce the results and compare their algorithms to mine. It has been utilized to perform the comparison between OBB's and DOP's in the VRAIS'98 paper.

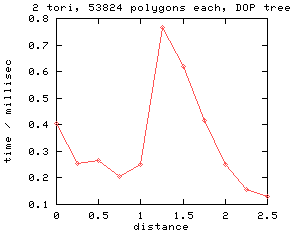
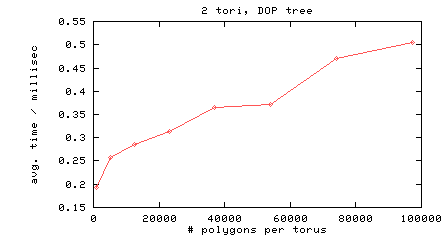
My test scenario involves two identical objects which are positioned at a certain distance from each other. The distance is computed between the centers of the bounding boxes of the two objects. Then one of them performs a full revolution about the z- and x-axis (z is pointing towards the viewer in the figure below) in a fixed, large number of small steps (usually, I use 2000). With each step a collision query is done, and the average collision detection time for that distance is computed. This procedure is done for different distances, which yields graphs as shown in the figures below.

Here is the source code of the "main loop" of my benchmark program bench.c, which I use for my benchmarks. And you might want to get this include file, also (vector math macros).
I'm afraid I can't make the collision detection code public domain (yet), but don't hesitate to contact me if you would like to consider some sort of cooperation.

Test suite

Here are some synthetic objects:

sphere torus cubes tetraflake

And here are some real-world CAD objects:

door (BMW) lock (BMW) Sharan (VW) pipes
3391 polygons 20898 polygons 60755 polygons 124544 polygons

Please contact me, if you would like to obtain them in Inventor format.

Sample plots

With the benchmark procedure described above, you get plots like the following:

The optimal number of orientations for DOP-trees

Here are some more plots showing various aspects of the DOP-tree algorithm. I have used them to determine the optimum number of orientations.
All plots have been derived from the same set of data.
The program for generating the data is the same as described above, except that only the "interesting" range of distances has been considered. The interesting range is the one around the "contact" distance. Here, I have considered the last two distance steps before the first distance with at least one collision, and the first two colliding distance steps.
The three postscript files contain the same plots with different "zoom" levels.

1.0 0.9 0.8

Comparison of Boxtrees, DOP-trees, OBB-trees, and QuickCD

I have also tried to compare 4 different collision detection algorithms: My Boxtree, my DOP-tree, OBB-tree (Rapid implementation), and QuickCD.
It seems that performance of OBB-trees and DOP-trees is about similar, while QuickCD and Boxtree have poorer performance.

The following postscript files show the results in more detail. The second section in each postscript file (entitled "time-vs-kompl") shows the performance of each algorithm depending on object type and complexity.

Each plot shows the same data, except with different zoom levels.

All timings have been done on a 194 MHz R10000 Onyx (IP25).

1.0 0.9 0.8

Performance of my "BBox-Pipeline Algorithm"

The following plots show the performance of my BBox-pipeline algorithm in more detail. As always, the plots are identical, except for a different zoom level.

All timings have been done on a 195 MHz R10000 Onyx2 (IP27).

1.0 0.9 0.8

Note that the cylinder ("zy") contains 2 very large polygons (compared to all the others, which have the same size); these are the bottom and top "lids", which consist of n vertices (n being the "sampling"). This might explain why the collision detection time increases so steeply with complexity.
It is funny that this algorithm exposes a behavior similar to the hierarchical algorithms with respect to complexity for the "SCHLOSS" object.

Movies about or using Collision Detection

Here are a few movies showing visualizing a collision detection algorithm, or an application of collision detection.

Description Movie Annot.
My separating planes algorithm in action MPEG (1.5 MB)  
Making an object slide along the surface of other objects. Here with a simple scene. MPEG (3.5 MB)  
    A small excerpt from the previous sliding movie. MPEG (300 kB)  
The sliding (gliding) simulation of some real-world objects.
The simulation used my DOP tree algorithm for collision detection. 		MPEG (4.8 MB)  
    A small excerpt from the previous sliding movie. MPEG (470 kB)  
    Another excerpt from the previous sliding movie. MPEG (100 kB)  
    Yet another excerpt from the previous sliding movie. MPEG (100 kB)  
Of course, I've got a torus chain simulation, too. MPEG (350 kB)  
This shows how a hierarchical collision detection algorithm works. Actually, it is a pretty old algorithm of mine (a very early version of the BoxTree), but the principle is the same. MPEG (1.3 MB)  
Another little demo with various objects. I call it the "Zoo" :-) MPEG (500 kB)  

All movies (except if otherwise noted) have first been filmed off the screen in real-time and then converted to MPEG, so that the full frame-rate was achieved. If your movie player plays them at 24 frames/sec, then you'll see exactly what I have seen on the screen.

(+) These movies were recorded using SGI's mediarecorder, which causes a decrease of frame-frate by a factor.

Publications

I've written several papers about collision detection and there is a chapter about it in my PhD thesis .

-----------------------------------------------------------

Gabriel Zachmann
Last modified: Fri Feb 23 15:50:13 MET 2007