Go to the Next or Previous section, the Detailed Contents, or the FS(E)L Home Page.
5.2.1 Generalised Transition Systems
The operational behaviour of a CSP process can be presented as a
transition system [Scat95].
A transition system is usually deemed to be a set of (effectively)
structureless nodes which have visible or
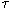 transitions to other nodes.
From the point of view of representing normal forms and other compressed
machines in the stable failures and failures/divergences models, it is
necessary to be able to capture some or all of the nondeterminism --
which is what the refusals information conveys -- by annotations on the
node.
This is a labelled transition system.
transitions to other nodes.
From the point of view of representing normal forms and other compressed
machines in the stable failures and failures/divergences models, it is
necessary to be able to capture some or all of the nondeterminism --
which is what the refusals information conveys -- by annotations on the
node.
This is a labelled transition system.
There is a duality between refusals (what events a state may not
engage in) and acceptances (what events a state must engage in,
if its environment desires): the one is the complement of the other in
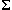 ,
the universe of discourse.
As components may operate only in a small subset of
,
the universe of discourse.
As components may operate only in a small subset of
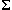 ,
and as it is inclusion between maximal refusals -- which corresponds to
reverse inclusion between minimal acceptances -- which must be checked,
it appears to be more efficient to retain minimal acceptance
information.
,
and as it is inclusion between maximal refusals -- which corresponds to
reverse inclusion between minimal acceptances -- which must be checked,
it appears to be more efficient to retain minimal acceptance
information.
We therefore allow nodes to be enriched by a set of minimal acceptance
sets and a divergence labelling.
We require that there be functions that map the nodes of a
generalised transition system as follows:
-
minaccs(P) is a (possibly empty) set of incomparable (under
inclusion) subsets of
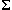 .
X
.
X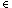 minaccs(P)
if and only if P can stably accept the set X, refusing all
other events, and can similarly accept no smaller set.
Since one of these nodes is representing more than one `state' the
process can get into, it can have more than one minimal acceptance.
In general (though not for normalised processes) it can also have
minaccs(P)
if and only if P can stably accept the set X, refusing all
other events, and can similarly accept no smaller set.
Since one of these nodes is representing more than one `state' the
process can get into, it can have more than one minimal acceptance.
In general (though not for normalised processes) it can also have
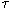 actions in addition to minimal acceptances (with the implicit
understanding that the
actions in addition to minimal acceptances (with the implicit
understanding that the
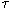 s
are not possible when a minimal acceptance is -- that is, that they
arise from stable states of the underlying machine
s
are not possible when a minimal acceptance is -- that is, that they
arise from stable states of the underlying machine
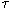 -reachable
from and assimilated within the "super-state").
However if there is no
-reachable
from and assimilated within the "super-state").
However if there is no
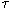 action then there must be at least one minimal acceptance, and in any
case all minimal acceptances are subsets of the visible transitions the
state can perform.
minaccs(P) represents the stable acceptances P can make
itself.
If it has
action then there must be at least one minimal acceptance, and in any
case all minimal acceptances are subsets of the visible transitions the
state can perform.
minaccs(P) represents the stable acceptances P can make
itself.
If it has
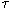 actions then these might bring it into a state where the process can
have other acceptances (and the environment has no way of seeing that
the
actions then these might bring it into a state where the process can
have other acceptances (and the environment has no way of seeing that
the
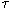 has happened), but since these are not performed by the node P
but by a successor, these minimal acceptances are not included among
those of the node P.
has happened), but since these are not performed by the node P
but by a successor, these minimal acceptances are not included among
those of the node P.
-
div(P) is either true or false.(13)
If it is true it means that P can diverge -- possibly as the
result of an infinite sequence of implicit
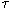 -actions
within P.
It is as though P has a
-actions
within P.
It is as though P has a
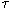 -action
back to itself.
This allows us to represent divergence in transition systems from which
all explicit
-action
back to itself.
This allows us to represent divergence in transition systems from which
all explicit
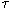 s
have been removed (such as normal forms).
s
have been removed (such as normal forms).
A node P in a generalised transition system can have multiple
actions with the same label, just as in a standard transition system.
These two properties, together with the initials (possible
visible transitions) and afters (set of states reachable after a
given event) are the fundamental properties of a node in the FDR2
representation of a state-machine.
Go to the Next or Previous section, the Detailed Contents, or the FS(E)L Home Page.
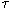 transitions to other nodes.
From the point of view of representing normal forms and other compressed
machines in the stable failures and failures/divergences models, it is
necessary to be able to capture some or all of the nondeterminism --
which is what the refusals information conveys -- by annotations on the
node.
This is a labelled transition system.
transitions to other nodes.
From the point of view of representing normal forms and other compressed
machines in the stable failures and failures/divergences models, it is
necessary to be able to capture some or all of the nondeterminism --
which is what the refusals information conveys -- by annotations on the
node.
This is a labelled transition system.
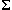 ,
the universe of discourse.
As components may operate only in a small subset of
,
the universe of discourse.
As components may operate only in a small subset of
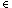 minaccs(P)
if and only if P can stably accept the set X, refusing all
other events, and can similarly accept no smaller set.
Since one of these nodes is representing more than one `state' the
process can get into, it can have more than one minimal acceptance.
In general (though not for normalised processes) it can also have
minaccs(P)
if and only if P can stably accept the set X, refusing all
other events, and can similarly accept no smaller set.
Since one of these nodes is representing more than one `state' the
process can get into, it can have more than one minimal acceptance.
In general (though not for normalised processes) it can also have