Closing a Million-Landmarks Loop
Simultaneous Localization and Mapping (SLAM) has been a topic of research for almost two decades by now after Smith, Self and Cheeseman first formulated it as an estimation problem for a state vector of landmark positions. While Smith et al. used a full n*n covariance matrix for n landmarks, many approaches tried to avoid the resulting O(n^2) update time by maintaining only individual covariances for each landmark. Julier and Uhlmann followed this idea with a particularly impressive result. Their algorithm maintains statistically consistent bounds and is so efficient they were able to estimate a 'million beacon map' in real time. Later it has been realized that correlations, i.e. uncertainty information not only for each landmark alone but also for their relative position, are crucial. We have earlier paraphrased this phenomenon as `certainty of relations despite uncertainty of positions'. It becomes most visible in closing a loop, because the precisely known relative position of adjacent landmarks forces the SLAM algorithm to distribute the error along the loop without introducing a break anywhere. In the last five years, many researchers have aimed at devising efficient approaches that maintain correlations. Several successful algorithms emerged, among them Relaxation,CEKF, SEIF, FastSLAM, Atlas, MLR, TJTF, Olson's stochastic descent algorithm, Dellaert's multifrontal-QR approach, and treemap. Our contribution was the latter; we feel that it is now time to pick up where Julier and Uhlmann left off and --- with the help of algorithmic progress and Moore's law --- close a million-landmarks loop.
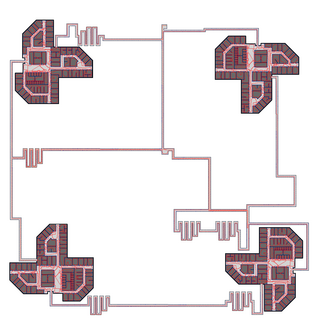
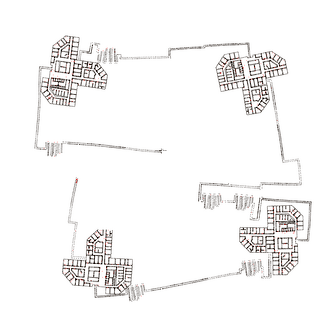
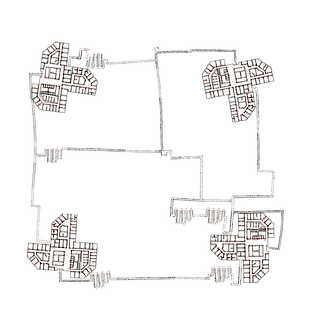
We simulate the robot moving through four 100-story-buildings, where the identical stories are taken from our university building (Universität Bremen, MZH, level 3). The robot uses elevators, modeled as pure vertical motion, to go from story to story. Still the mapping is 2D, the stories are simply counted. The robot starts in the middle of the map and consecutively maps the left-upper, right-upper, right-lower and left-lower building, connected on the ground level by corridors. Then it closes a huge loop through all four buildings. The left image shows the true map (ground floor) used for simulation with landmarks (blue), robot trajectory (red) and elevators (green). The middle image shows the map estimate before closing the final loop, the right shows the estimate after closing the loop. The loop closure took 21ms when computing only an estimate for the ground floor (10000 landmarks) or 442ms for computing an overall estimate (AMD Athlon 64, 2.2GHz).
This video shows the mapping process as a 3-D animation (2D SLAM + Z coordinates by counting stories). You can see the robot going through all four skyscrapers. In the end, when the video slows down, the algorithm closes several loops. This yields new information on the position of the skyscrapers and makes them "jump" in the estimate.
More detailed information is found in my in our IROS 2006 paper. the corresponding IROS 2006 talk and a recent talk at university of Zaragoza.